Linear regression part one - linear quadratic loss minimizer.

If there is one thing statisticians are good at, it is drawing straight lines. (Peter Mueller deserves the credit for that – he said it in a lecture once.)

I write this partly to get the blog up and running, and partly because it’s good to begin at the beginning.

Suppose you have a graph that looks like this: 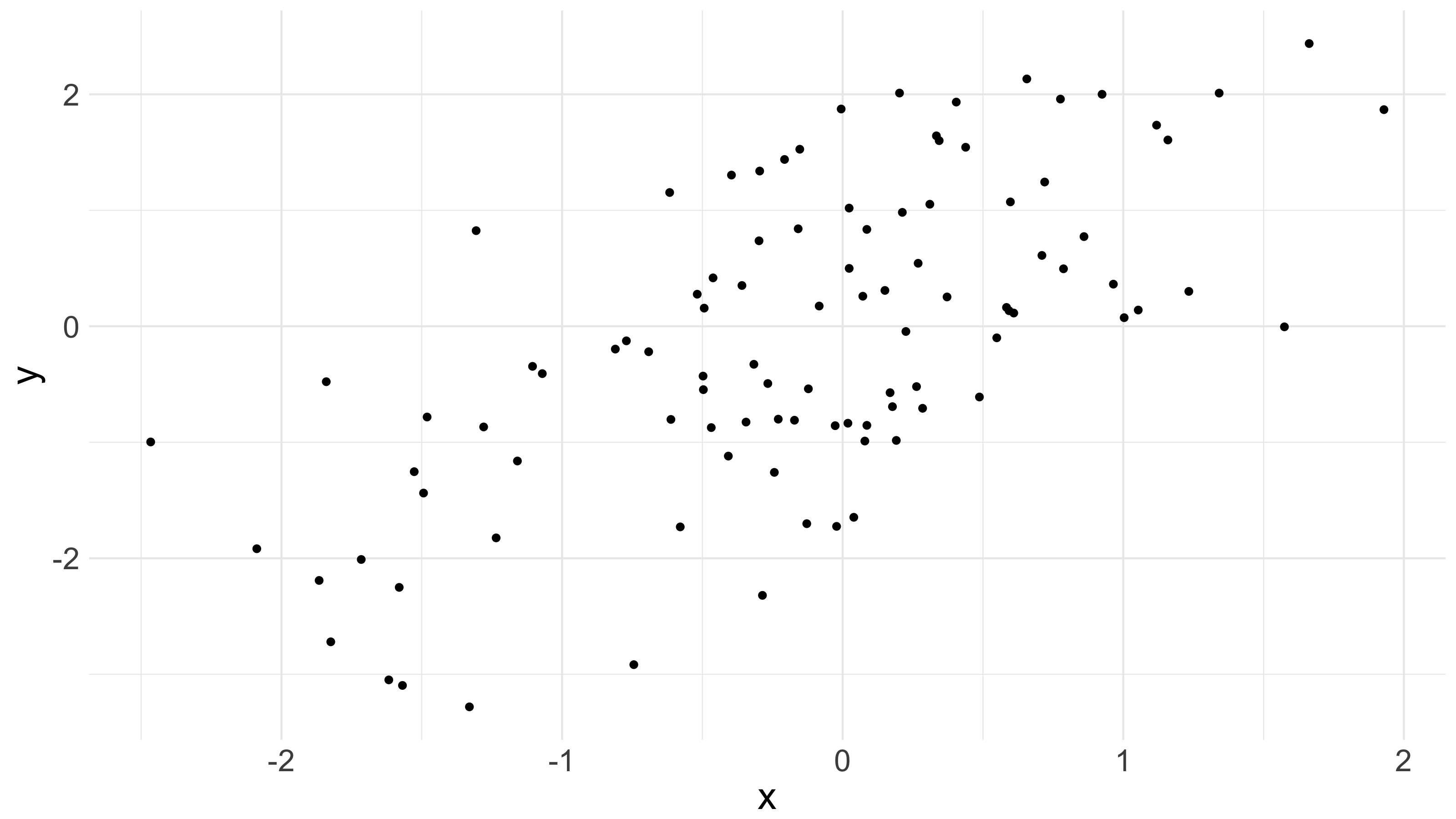And suppose you wanted to capture the data on that graph, as well as possible, using a linear function of $x$ – i.e., something of the form $\beta_0 + \beta_1 x$. You might imagine that you would like a friend, who has access to all of the $x$ values of the points above, to recover the corresponding $y$ values, but that you only have enough bandwidth to transmit a slope and an intercept.

Now, suppose further that the cost you pay for any error in your friend’s estimate is proportional to the squared error between her guess - based on the slope and intercept you provided – and the true $y$ value.

In that situation, the “best” line is the one that minimizes quadratic loss – the sum of the squared vertical distances between each point and the line in question. So you want to find $\beta_0$ and $\beta_1$ which satisfy:

$$\begin{align*} argmin_{\beta_0, \beta_1} \sum_i (y_i - (\beta_0 + \beta_1x_i))^2 \end{align*}$$

Equivalently, if we let

$$\begin{align*} Y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}, \quad X = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix}, \quad \text{and } \beta = \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} \end{align*}$$

then the best line is the one that minimizes

$$argmin_\beta (Y - X\beta)'(Y - X\beta).$$

To find that minimum, first notice that because $\beta'X'Y$ is a scalar, and hence because $(\beta'X'Y)' = Y'X\beta = \beta'X'Y$,

$$\begin{align*} (Y - X\beta)'(Y - X\beta) &= Y'Y - \beta'X'Y - Y'X\beta + \beta'X'X\beta \\ &= Y'Y - 2\beta'X'Y + \beta'X'X\beta \end{align*}$$

So, to find the $\beta$ which minimizes quadratic loss, take partials of that last, set them to zero, and solve:

$$\begin{align*} &\frac{\partial}{\partial \beta} (Y - X\beta)'(Y - X\beta) = -2X'Y + 2X'X\beta = 0 \\ &\Rightarrow X'X\beta = X'Y \\ &\Rightarrow \beta = (X'X)^{-1}X'Y \end{align*}$$

The last step is kosher so long as $X'X$ is invertible.

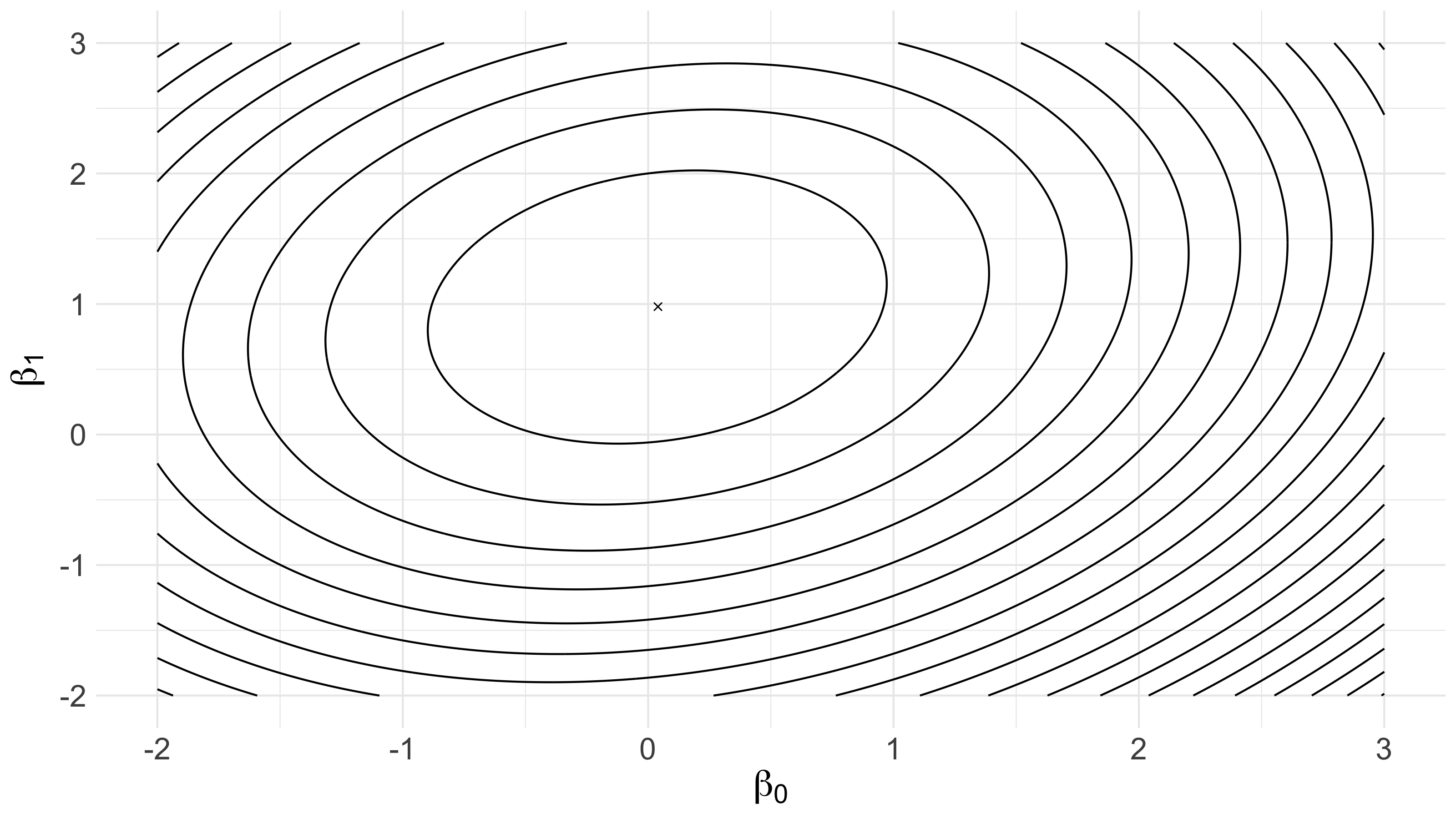
Regarding the data in the scatterplot above as fixed, the contour plot below shows the value of the quadratic loss function, $\sum_i (y_i - (\beta_0 + \beta_1x_i))^2 = (Y - X \beta)'(Y - X\beta)$ for differing values of $\beta_0$ and $\beta_1$. The tiny ‘x’ marks the unique minimum we just found, $(X'X)^{-1}X'Y$.

And the line through our points, which corresponds to that choice of $\beta_0$ and $\beta_1$, is drawn in the below picture. 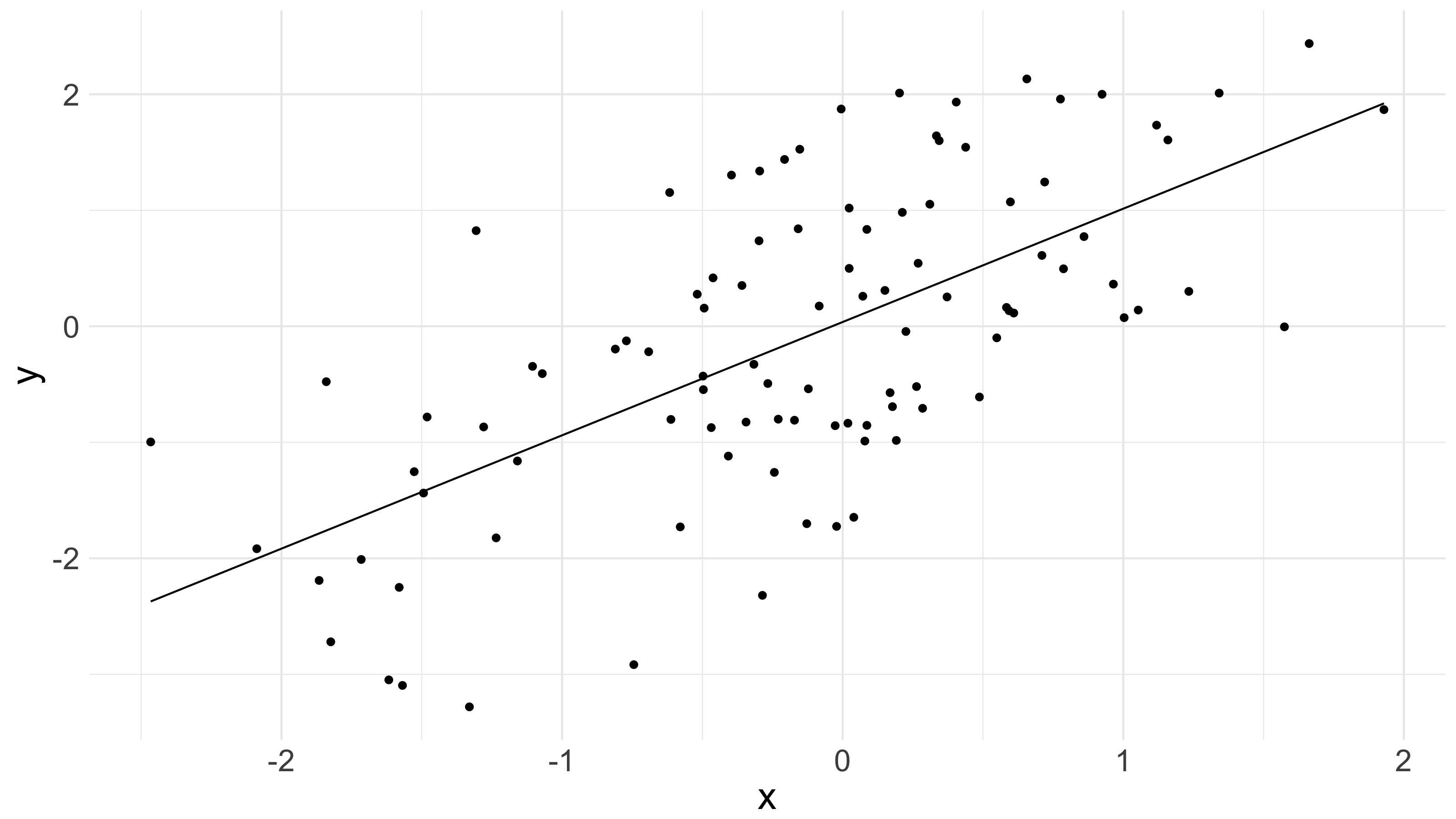Voila.

Notice there was nothing stochastic in anything above - no assumptions about a probability distribution governing $Y$ or $X$, or normally distributed epsilons or anything like that. If what you care about is quadratic loss, then $\beta = (X'X)^{-1}X'Y$ gives you the best line through your points, probability distributions be damned.

---

Some R code below. Simulate some data, then find and plot the line which minimizes quadratic loss for that data.

require(ggplot2)

## Simulate some data. X[,2] ~ N(0, 1), Y ~ N(X[,2], 1).
X <- matrix(c(rep(1, 100), rnorm(100)), ncol = 2)
Y <- rnorm(100, mean = X[,2])

## Find (X'X)^(-1)X'Y.
beta_hat <- solve(t(X) %*% X) %*% t(X) %*% Y

## Plot the data, with the regression line.
df <- cbind.data.frame(x = X[,2], y = Y)
ggplot(df, aes(x = x, y = y)) + 
  geom_point() + 
  stat_function(fun = function(x){beta_hat[1] + beta_hat[2]*x}) +
  theme_minimal() + 
  theme(text = element_text(size = 20))